4D-LRM:
Large Space-Time Reconstruction Model From and To Any View at Any Time

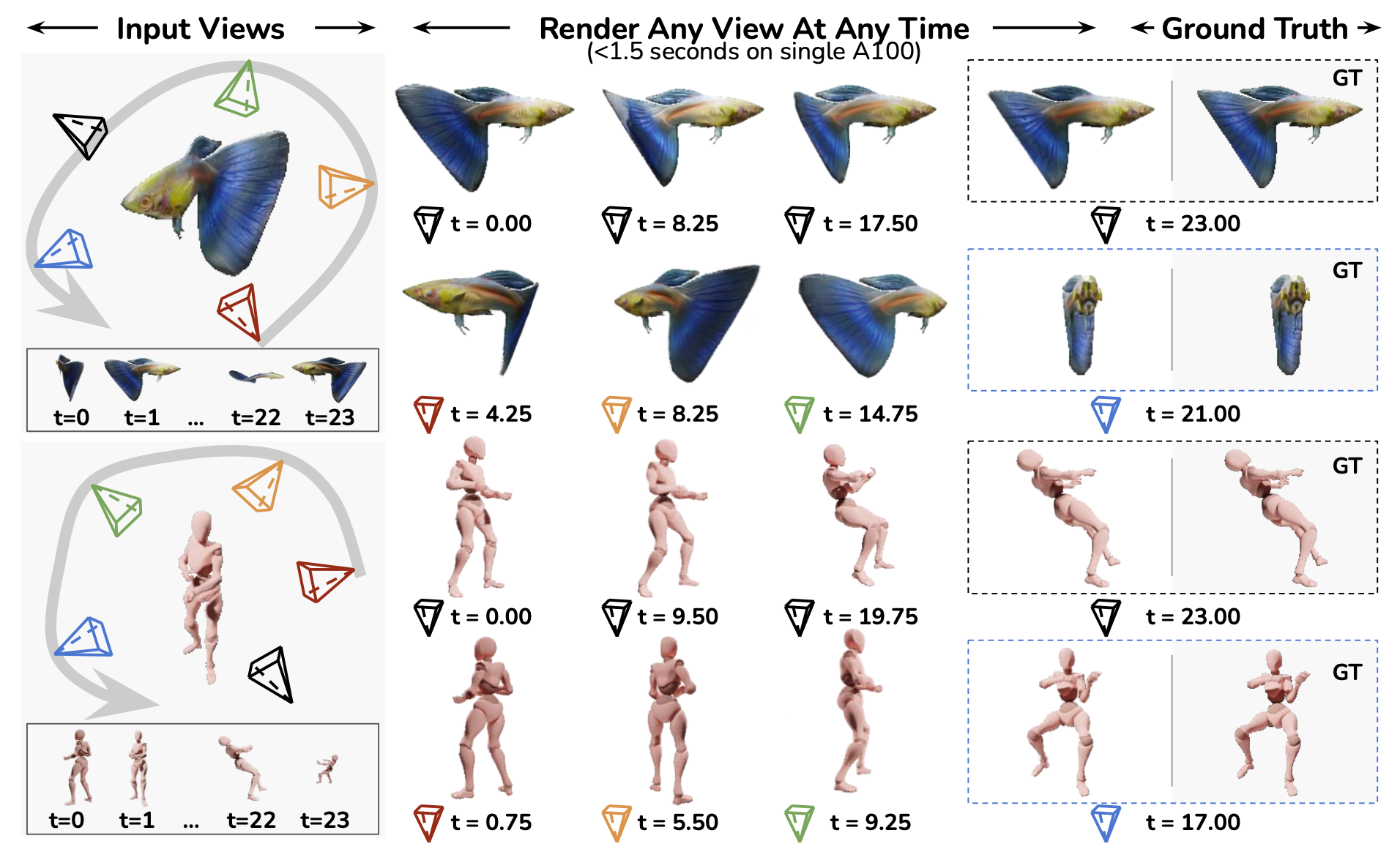
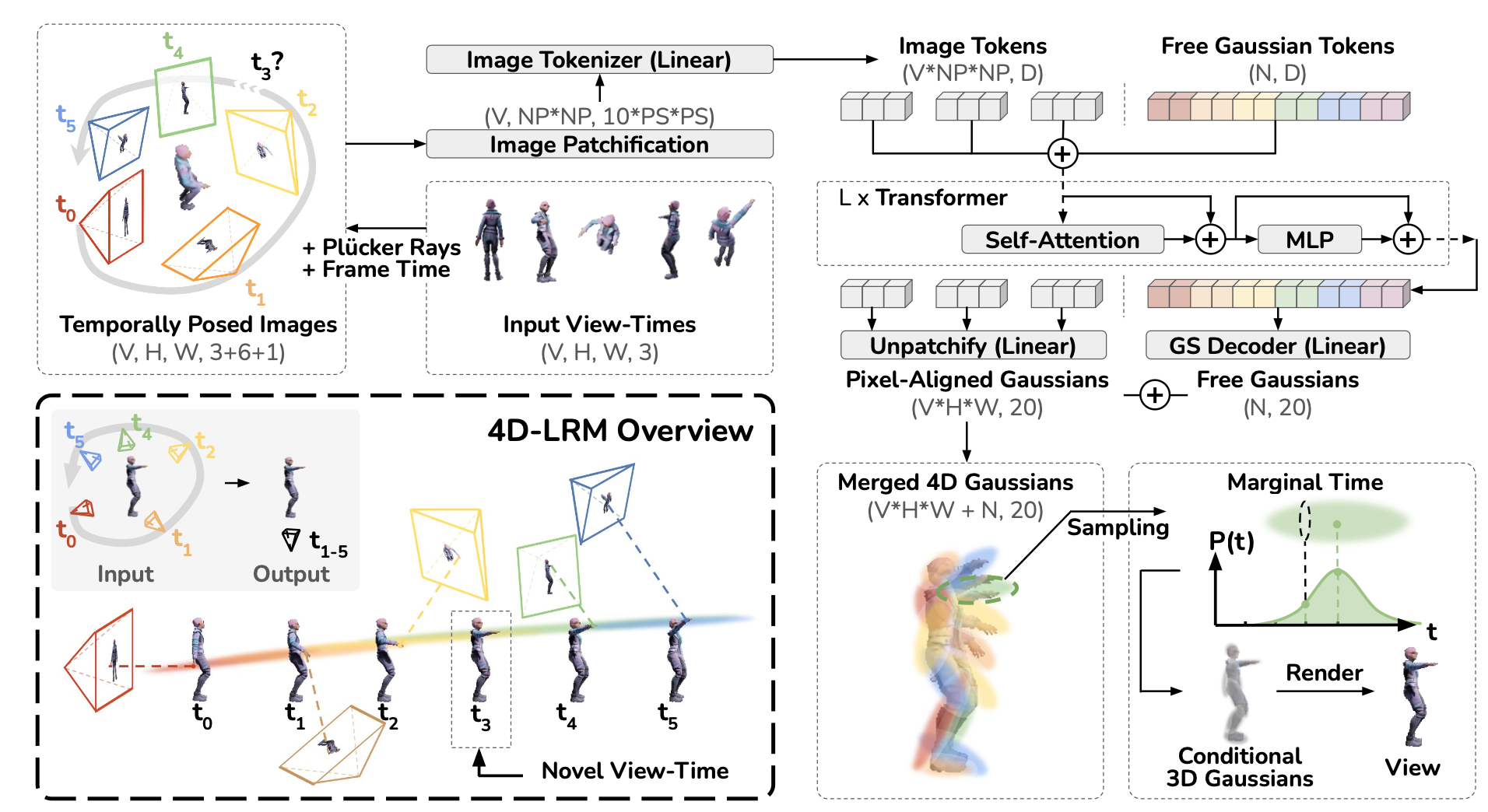
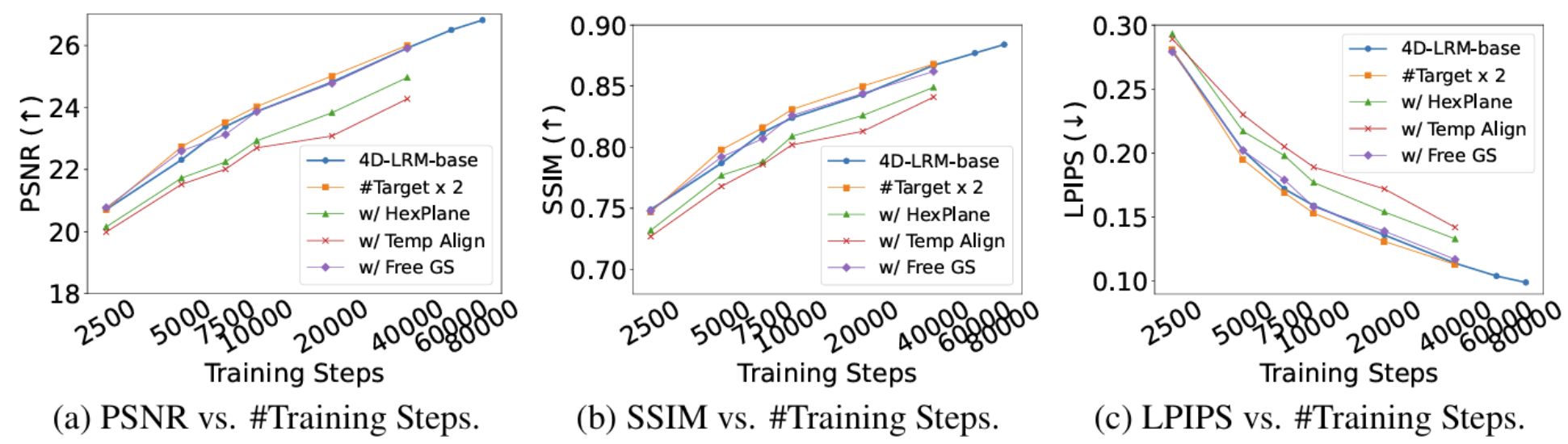
Can we scale 4D pretraining to learn general space-time representations that reconstruct an object from a few views at some times to any view at any time? We provide an affirmative answer with 4D-LRM, the first large-scale 4D reconstruction model that takes input from unconstrained views and timestamps and renders arbitrary novel view-time combinations. Unlike prior 4D approaches, e.g., optimizationbased, geometry-based, or generative, that struggle with efficiency, generalization, or faithfulness, 4D-LRM learns a unified space-time representation and directly predicts per-pixel 4D Gaussian primitives from posed image tokens across time, enabling fast, high-quality rendering at, in principle, infinite frame rate. Our results demonstrate that scaling spatiotemporal pretraining enables accurate and efficient 4D reconstruction. We show that 4D-LRM generalizes to novel objects, interpolates across time, and handles diverse camera setups. It reconstructs 24-frame sequences in one forward pass with less than 1.5 seconds on a single A100 GPU.

We observe that increasing the number of target views slightly improves convergence speed, though at the cost of increased iteration time. Introducing free Gaussians from scratch does not significantly impact reconstruction quality but substantially slows down training. Additionally, we find that the 4DGS representation with 3DGS + HexPlane is less expressive than the unified space-time formulation, which informed our final design choice. We also note that enforcing strict temporal alignment degrades performance, whereas pixel alignment improves reconstruction quality. This supports our earlier observation that 4D-LRM effectively redistributes Gaussians to unseen time intervals to handle sparse temporal supervision.

1. 4D-LRM-Base: Transformer with 768 hidden dimensions, 12 layers, and 12 attention heads, trained with 12 random input views and 12 random target views. No free Gaussians.
2. #Target x 2: Trained with 12 random input views and 24 random target views.
3. w/ Hexplane: Instead of unified space-time representation, an alternative 4DGS representation with decomposed neural voxel encoding inspired by HexPlane.
4. w/ Temp Align: Similar to the idea of pixel-aligned Gaussians, we force μ_T to the input frame time, reducing the parameterization to dim_4DGS = 19.
5. w/ Free GS: Trained with N = 1024 free Gaussian tokens from scratch.

We analyze inference-time scaling as the number of input views varies. In terms of PSNR and SSIM, performance improves with more input views and peaks at 48, after which it begins to decline slightly. We attribute this to two factors: (1) excessive Gaussians may overcrowd the 4D representation, reducing its quality, and (2) the Transformer struggles with very long input sequences. This observation suggests a promising future direction: designing 4D-LRM variants that can handle longer contexts with hybrid models (Long-LRM) and incorporate test-time training (LaCT).